神经网络的实现

如何实现一个神经网络

神经网络的表示

单隐藏层神经网络

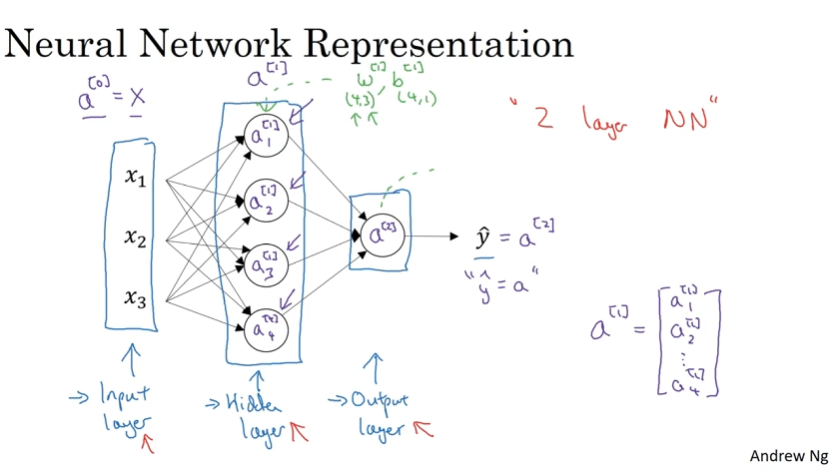
输入层

输入层有三个输入单元，分别为$x_1,x_2,x_3$，输入层的输出为$a^{[0]}$，即$a^{[0]}=x$，其中$x$为输入向量，$x=\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}$

隐藏层

隐藏层有四个隐藏单元，分别为 $a_1^{[1]},a_2^{[1]},a_3^{[1]},a_4^{[1]}$ ，隐藏层的输出为$a^{[1]}$，即 $a^{[1]}=\begin{bmatrix}a_1^{[1]}\\a_2^{[1]}\\a_3^{[1]}\\a_4^{[1]}\end{bmatrix}$

输出层

输出层有两个输出单元，分别为 $a_1^{[2]},a_2^{[2]}$，输出层的输出为$a^{[2]}$，即 $a^{[2]}=\begin{bmatrix}a_1^{[2]}\\a_2^{[2]}\end{bmatrix}$

计算神经网络输出

对于第一层神经网络，如果输入是一组x向量，我们就有
$z^{[1]}=W^{[1]}x+b^{[1]}$
$a^{[1]}=\sigma(z^{[1]})$
$z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$
$a^{[2]}=\sigma(z^{[2]})$

其中$W^{[1]}$是第一层的权重矩阵，$b^{[1]}$是第一层的偏置向量，$W^{[2]}$是第二层的权重矩阵，$b^{[2]}$是第二层的偏置向量，$\sigma$是激活函数，这里使用的是sigmoid函数，$z^{[1]}$是第一层的输入向量，$a^{[1]}$是第一层的输出向量，$z^{[2]}$是第二层的输入向量，$a^{[2]}$是第二层的输出向量